2023年10月19日

AAVE：Liquidationの分析～Health Factorの維持水準を考える～

Ledefiリサーチ事業部

DeFi（分散型金融）

はじめに
清算イベントの整理
　2.(1) 清算確率
　2.(2) 清算確率の分析方法
清算確率の定式化
　3.(1) 分析で考慮すること
　3.(2) 数理モデルの構成
　3.(3) 変動率および相関の水準
数値解析的考察
　4.(1) 清算確率算出結果
　4.(2) 全般的傾向
　4.(3) 個別的分析
おわりに
参考文献
Appendix 1. 数値検証スクリプト

1. はじめに

弊社レポート「Aave：Liquidity Protocolの基本」（[1]）では、AAVEを用いた担保付借入の仕組みについて、基本的な内容を説明した。本レポートでは、借入を用いた運用を行う際の、重要な要素である「清算（liquidation）」について、考察を実施する。

清算とは、担保の価値が棄損したときに、差し入れた担保の一部が強制的に現金化されることで、ペナルティを徴求されることから、AAVE運用では絶対に避けるべきものである。レポートの具体的な目標は、ある状況下で清算が発生する確率（清算確率）をモデル化して、数値解析的な考察を行うことである。

なおモデルには多くの仮定を含むため、清算確率の数値は絶対的なものではなく、相対的なものとして扱う必要がある。読者におかれても、この点は注意されたい。

Keywords: AAVE, liquidation, Health Factor, diffusion process, numerical analysis
（AAVE, 清算, 健全性指標, 拡散過程, 数値解析）

[END OF PUBLIC CONTENTS]

2. 清算イベントの整理

清算確率
[1]に示す通り、AAVEでの担保付借入では、担保の価値が借入の価値を上回ることが求められる。清算の判定は、次の式で定義する健全性指標（Health Factor）によって管理される。

HealthFactor=\frac{\sum_{i=1}^n Col_{i}^{ETH}×TH_{i}}{\sum_{j=1}^mLoan_{j}^{ETH}} \tag{1}

Health Factorの式において、分子の Col_i^ETHは担保資産のイーサリアム建て価格、TH_i は担保資産 i に対する清算閾値、分母の Loan_j^ETH は借入資産のイーサリアム建て価格である。

Health Factorが1以上のときは、借入に必要なコストは利子だけである。一方でHealth Factorが1を下回ると、その瞬間に一定量の担保が強制的な清算（liquidation）にかけられて、利子に加えて清算手数料（liquidation bonus）を徴求される。清算手数料は実質的にはペナルティであり、担保の数%～数十%になるので、AAVEを使うときはHealth Factorを1より必要十分に高く保ち、清算を起こさないことが最も重要な原則になる。言い換えると、現在のHealth Factorの水準（これを初期状態「HF0」という）から、一定の期間の間に清算が発生する状況（清算確率）を調べることが、AAVE分析の基礎になる。

2.(2) 清算確率の分析方法

清算確率を分析する方法としては、実観測データを用いる方法と、数理モデルを用いる方法が考えられる。本レポートでは、後者の数理モデルを用いた分析について考察結果を解説するが、まずは双方について概要を説明する。

2.(2).a 実観測データを用いた分析

実観測データを用いた分析としては、例えば、AAVEのユーザー数と清算発生の件数から、一定期間のうちに清算が発生する確率を推定することや、ユーザーのHealth Factorの分布から、およそ市場で受け入れられるHealth Factorの水準を推定することが考えられる。
また、実際に清算が発生したポートフォリオを過去に遡り、清算の一定期間前のHealth Factorの水準を調べることで、いわゆる事後確率を推定することも有用と考える。

2.(2).b 数理モデルを用いた分析

数理モデルを用いた分析としては、Health Factorの構成要素である担保資産および借入資産の変動をモデル化する方法や、Health Factorそのものをモデル化する方法がある。これに対して、Health Factorは担保資産や借入資産の構成によって特性が変化することから、構成要素の担保資産および借入資産をモデル化してHealth Factorを算出することが現実的と考える。

ここで、担保資産や借入資産をモデル化するときの注意点としては、できるだけ解析しやすいモデルから取り組むということである。例えば、担保資産も借入資産も、一般にその変動は非連続的な変化を伴うものになりがちである。しかしながら、そういったモデルは構築が難しく、分析のためのパラメーターを与えるのにも困難を伴う。それであれば、比較的簡便な方法でモデルを構築し、パラメーターにストレスをかけることで耐性を確認する方が、有益な分析結果が得られると考える。

また、数理モデルを使用する場合の注意点として、モデルには多くの仮定を含むことになるため、算出された確率を絶対的なものとして扱うことは困難である。それよりも、同一の仮定のもとで条件を変えた時の相対的な変化を中心に見ることが肝要である。

3. 清算確率の定式化

3.(1) 分析で考慮すること

清算確率を分析するには、どのようなことを考慮すればよいか？
まず清算判定の基礎となる健全性指標（Health Factor）の構成要素は、分子が担保資産と清算閾値（定数）の掛け算、分母が借入資産であった。したがって、まず分子と分母それぞれの変動を考えることが必要であろう。また、分数式では、分子と分母の変動を同時に捉える必要がある。したがって、両者の動きの関連性、即ち相関を考えることも必要になる。

続いて、時間はどうであろうか。Health Factorが低下するという危険の兆候が発生し、その兆候を察知したユーザーは、借入金を返済するか、担保資金を補充することになる。この点、通常AAVEで借り入れた資産は、別の商品で運用されている。そうすると、危険の兆候を察知したユーザーは、まず借入資産の運用を中止し、資産を回収したうえでAAVEの借入金を返済することになる。もしくは、別の方法で資金を入手し、担保金を補充することになる。

これらの、兆候の発生、兆候の察知、返済資産もしくは必要資金の手当て、借入金返済もしくは担保補充の実施、の一連の動作に係る時間を、Health Factorが変動する時間として考慮する必要がある。以下、分析で考慮する、兆候の発生から借入金返済もしくは担保補充実施までの期間のことを「保有期間」と表現する。なお以降の計算では、保有期間の間、ユーザーはAAVEのポジションを操作できないことを前提にしている。

清算確率を分析するにあたり考慮する事項をまとめると、次の通りである。
・担保資産の変動率（分子の変動率）
・借入資産の変動率（分母の変動率）
・担保資産と借入資産の相関（分子と分母の相関）
・保有期間
このうち、前3者は市場環境として与えられるものであり、ユーザーにできることは、資産の選択と組み入れ比率になる。一方で保有期間は、ユーザーの運用体制やオペレーションの巧拙によって定まるものであり、その短縮は、ユーザーがかけられるコストを考慮して決定するものである。

3.(2) 数理モデルの構成

3.(2).a 担保資産・借入資産の計算式

今回は、担保資産と借入資産のそれぞれが、単純な拡散過程（対数正規分布）に従うとしてモデル化する。すなわち、借入資産 X を、担保資産を Y と表すと、Health Factor HF を、

dX_{t}=\sigma_{X}(X_{t})X_{t}dW_{t}^X \tag{2}

dY_{t}=\sigma_{Y}(Y_{t})Y_{t}dW_{t}^Y \tag{3}

HF_{t}=\frac{Y_{t}}{X_{t}} \tag{4}

とモデル化する。このとき $W_t^X$ および $W_t^Y$ は、相関を持ったウィナー過程である。また借入資産および担保資産ともに複数銘柄の保持が認められているところ、ここでは、そのポートフォリオが拡散過程に従うとしている。

そのうえで、計算はモンテカルロ・シミュレーションで実施する。なお数値計算においては、保有期間を日数で設定することから、 $σ_X(X_t )$ および $σ_Y(Y_t )$ も、日率の変動率を与えることにするとともに、両者とも期中で一定の値として $σ_X(X_t )=σ_X,σ_Y(Y_t )=σ_Y$ を適用する。

3.(2).b 清算確率の計算式

保有期間を T 日とするとき、清算確率 p は、健全性指標の初期値 $Z_0=Y_0/X_0$ を用いて、

p(Z_0)=P(τ≤T|HF_0=Z_0),τ=\underset{t}{min}{HF_t<1} \tag{5}

と表すことができる。ここで τ は、数学的には stopping time と呼ばれる確率変数である。
清算の発生を考える場合、(2)式に示す通り、保有期間の満期 T までにHealth Factorが1を下回る状況全てを対象にする必要がある。しかしながら期中の連続的な変動を考慮することは検証の負荷が高くなるため、今回は保有期間の満期時点においてHealth Factorが1を下回る状況を対象にする。数式で表すと、

p(Z_0)=P(HF_T<1|HF_0=Z_0) \tag{6}

である。

3.(3) 変動率および相関の水準

2023年9月現在の市況でBTC-USDの日率変動率を推定すると、2.4%になった。したがってこのレベルを、日次変動率を考える開始点としてよいだろう。そのうえで変動率の設定には、日中価格の影響を織り込む必要がある。

これは、清算は終値ではなく日中価格に基づいて常に実行されるため、変動率には日中変動を考慮した値を適用する必要があるということである。過去データを用いる場合は、日中最高値と最安値を考慮した変動率になる。一方で日中変動を考慮した変動率の推定は、データ量および取り扱い方法の両方の点で難易度が高く、本レポートの範囲を超える内容になる。そのため深い言及は行わないが、2倍等の数値（すなわち5.0%等）になることもあり得る点は、配慮するとよいであろう。

また、市場急変時の影響を見るという点では、日中変動の考慮による変動率の加算とは別に、急変時の変動率を考慮することも有用である。例えば2022年11月のFTXショック時の暗号資産変動率が高いことは広く知られた事実である。これは、通常期の変動率とは別に、ストレス期の変動率として調整した変動率を適用することから開始すると良いだろう。

また、担保資産と借入資産の変動の相関も与える必要がある。この点、相関の推定は、変動率の推定以上に安定性が欠落するものであるため、推定を行うよりも外形的に与えた数値で分析を行うのが良いであろう。すなわち、相関＝0.0, 0.5, 0.95等を所与の数値として計算したうえで、実際の運用の時の投資判断の材料の一つにするということである。

4. 数値解析的考察

4.(1) 清算確率の算出結果

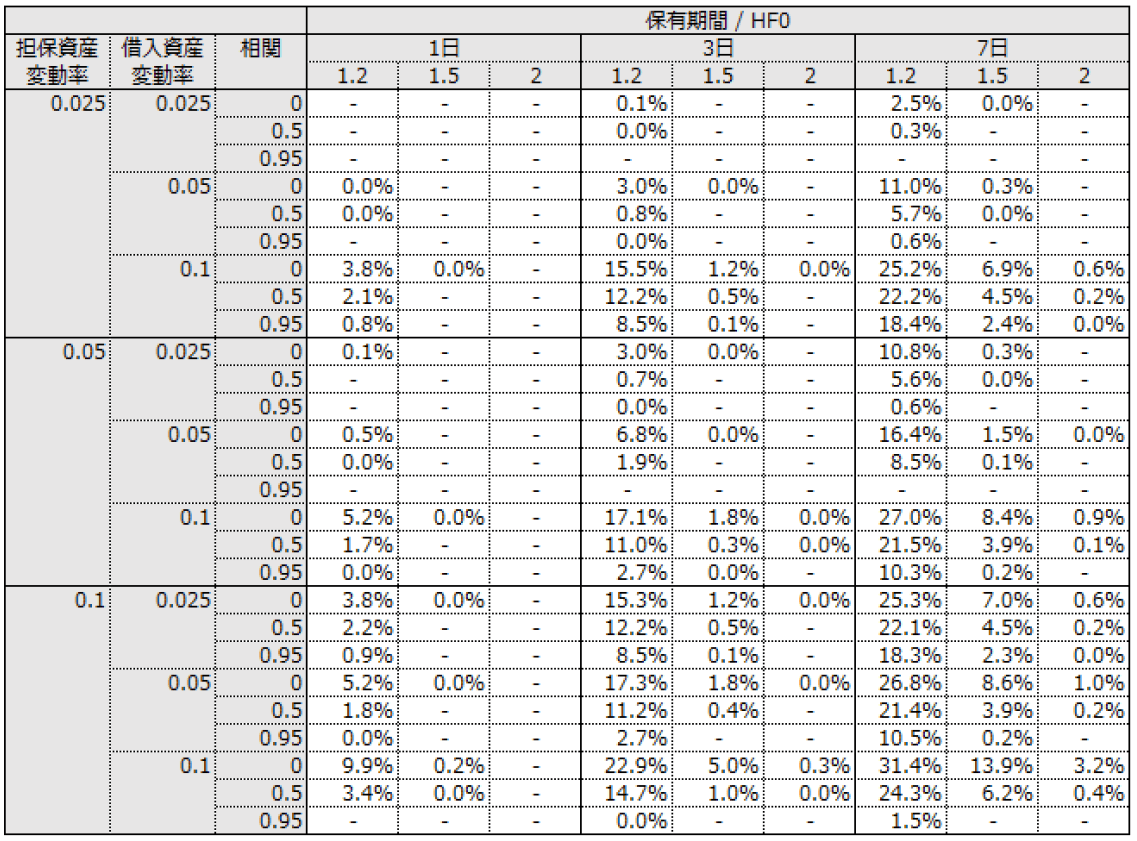
はじめに、前章の定式化の内容を、変動率として日次2.5%、5.0%、10.0%、相関として0.0、0.5、0.95としたときの清算確率の算出結果（モンテカルロ・シミュレーションによるもの）を表1.に示す。ここで、保有期間は1日、3日、7日の3種類、Health Factorの初期値HF0も1.2、1.5、2.0の3種類を用意した。また表1.において、”-“は試行における清算の発生が1件もなかったことを意味し、”0.0%”は正値の回数の清算が発生したが、百分率表示での四捨五入によって0.0%になったことを意味する。

表 1. 清算確率の試算結果

出所：Next Finance Techにて作成

表の見方は、各行は資産の状況を表している。特に変動率と相関は、市場において決定され、ユーザーが能動的に調整することができないものである。これに対し、保有期間と健全性指標の初期値HF0は、ユーザーがリスク選好に基づいて能動的に調整する戦略であることに注意したい。したがって、担保資産と借入資産が決まっているときは、該当する行の中で、保有期間および初期値HF0の横比較を行うように目線を動かすと良い。

以下、表1.で特に保有期間を3日間としたときの清算確率の変化について、低変動率（変動率＝0.025）、中変動率（同0.05）、高変動率（同0.10）の3パターンにつき、図1.から図3.にプロットする。ここで同一図内の複数の折れ線は、相関の違いを意味している。

図 1. 清算確率（低変動率、σ=2.5%）

図 2. 清算確率（中変動率、σ=5.0%）

図 3. 清算確率（高変動率、σ=10.0%）

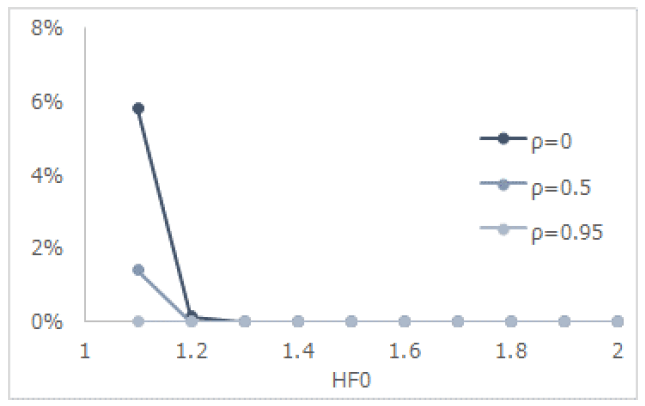
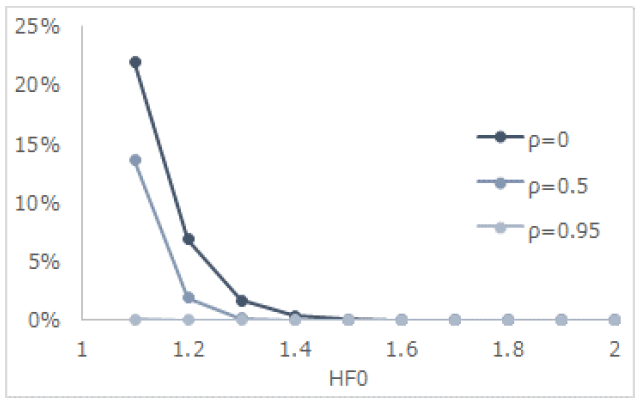
4.(2) 全般的傾向

まず、全般的傾向として言えることは、次の3点である：
・HF0が高いほど、清算確率は低くなる
・変動率が高いほど、清算確率も高くなる
・相関が高いほど、清算確率は低くなる

一点目は当然の帰結であろう。構築時点での健全性指標が1に近ければ清算確率は高まり、1よりも大きくなるほど清算確率が低くなることが、数値計算によっても示されたということである。

また二点目も、わかりやすい結果であろう。他条件が同じ場合、変動率が高い方が値の分布は広がることになり、したがって健全性指標が1を下回る確率が高くなる（＝清算確率が高くなる）というものである。

三点目は、考え方に慣れる必要があるが、理論的に整合的である。すなわち、相関が高いということは分子と分母の動きが相殺されるということであり、結果として健全性指標の動きは小さくなるということになる。相関が高い場合の極端な例としては、米ドルに連動するステーブルコインを担保に、米ドルに連動する別のステーブルコインを借り入れるケースが挙げられる。この場合、分子も分母もともに実質的に米ドル資産であるため、米ドルとイーサリアムの交換レートがどのように変化しても、分数で表される健全性指標はほとんど変化しないことがわかるであろう。逆に担保資産と借入資産の相関が低い場合は、それぞれの資産の変動率が同一であっても、健全性指標の変動率は高くなり、清算確率も上昇することが、各グラフの折れ線の水準の違いから読み取ることができる。

4.(3) 個別的分析

続いて、表1.における清算確率の数値を見ながら、保有期間に応じたHealth Factorの適切な水準を考察する。

まず、保有期間が1日の場合（すなわち、1日でポジションの解消ができる場合）、Health Factorの水準HF0を1.5に保ったときの清算確率は0.2%であり、同じく2に保ったときは、計算上の清算は発生しないことになる。したがって、このモデルの環境であれば、水準を1.5に保つことは十分に安全と言えるだろう。一方でHF0を1.2まで引き下げたときは、一部の市場環境で5%や9%といった清算確率が確認されており、危険であると判断できる。

続いて、保有期間が3日の場合、HF0を1.5に保った状況でも、一部の市場環境では1%を超える清算確率が確認され、変動率の高い状況では5%の確率も確認される。ただし、全般的には1%を下回る確率であり、担保資産や借入資産に係る市場環境を十分に確認したうえでHealth Factorの維持水準を決定する必要があるだろう。なお、保有期間が3日の場合でもHF0を2に保ったときの清算確率は十分に小さいと言える。

最後に、保有期間が7日の場合、HF0を1.5に保った状況でも、かなりの市場環境において、有意に高い水準の清算確率が確認されている。HF0を2に保ったときは、清算確率は概ね1%を下回るが、全体的に清算の可能性が高くなることに相違はない。もとよりHF0を2に保った場合、担保資産の利用効率性はかなり下がることから、保有期間に7日を必要とする状況では、投資判断そのものの要否を検討した方がよい水準になると考える。

5. おわりに

本レポートでは、AAVEの使用時に考慮する強制的な清算（liquidation）の発生、言い換えると清算確率について、数値解析による考察を行った。

清算確率に影響を与える要素を再掲すると、担保資産の変動率、借入資産の変動率、資産間の相関、およびポジションの解消にかかる保有期間である。前3者を市場における所与の値、後者を自身のおかれた環境としたうえで、Health Factorの維持すべき水準（HF0）を考察すると、保有期間が1日であるときは1.5に維持することで問題なく、3日であるときは市場環境に注意したうえで1.5を選択可能、一方で7日であるときは1.5でも清算確率が高く投資判断自体を検討した方が良いことが分かった。

もちろん、上記の結果は単純化したモデルでの結果であるということ、また特性の良い分布（対数正規分布）を用いていることから、現実の市場環境においては、より厳しい結果になることも予想できるだろう。しかしながら、清算についての理解を得るには有用な内容であると考えており、読者におかれては、必要に応じてモデルを拡張し、考察を深めて頂きたい。

参考文献

[1] Next Finance Tech，Aave：Liquidity Protocolの基本．2023．
[2] AAVE Project，Aave Document Hub．（オンライン）（引用日: 2023 年8 月22 日．）
https://docs. Aave .com/ hub/．
[3] Aave Project，Aave Protocol Whitepaper V2.0．2020．
[4] Emilio Frangella, Lasse Herskind，Aave V3 Technical Paper．2022．

Appendix 1. 数値検証スクリプト

本分析において使用した数値検証のPythonスクリプトを、抜粋して転記する。本文に示した数式理解の参考にされたい。